异或（XOR），是一个数学逻辑运算。如果a、b两个值不相同，则异或结果为1。如果a、b两个值相同，异或结果为0。

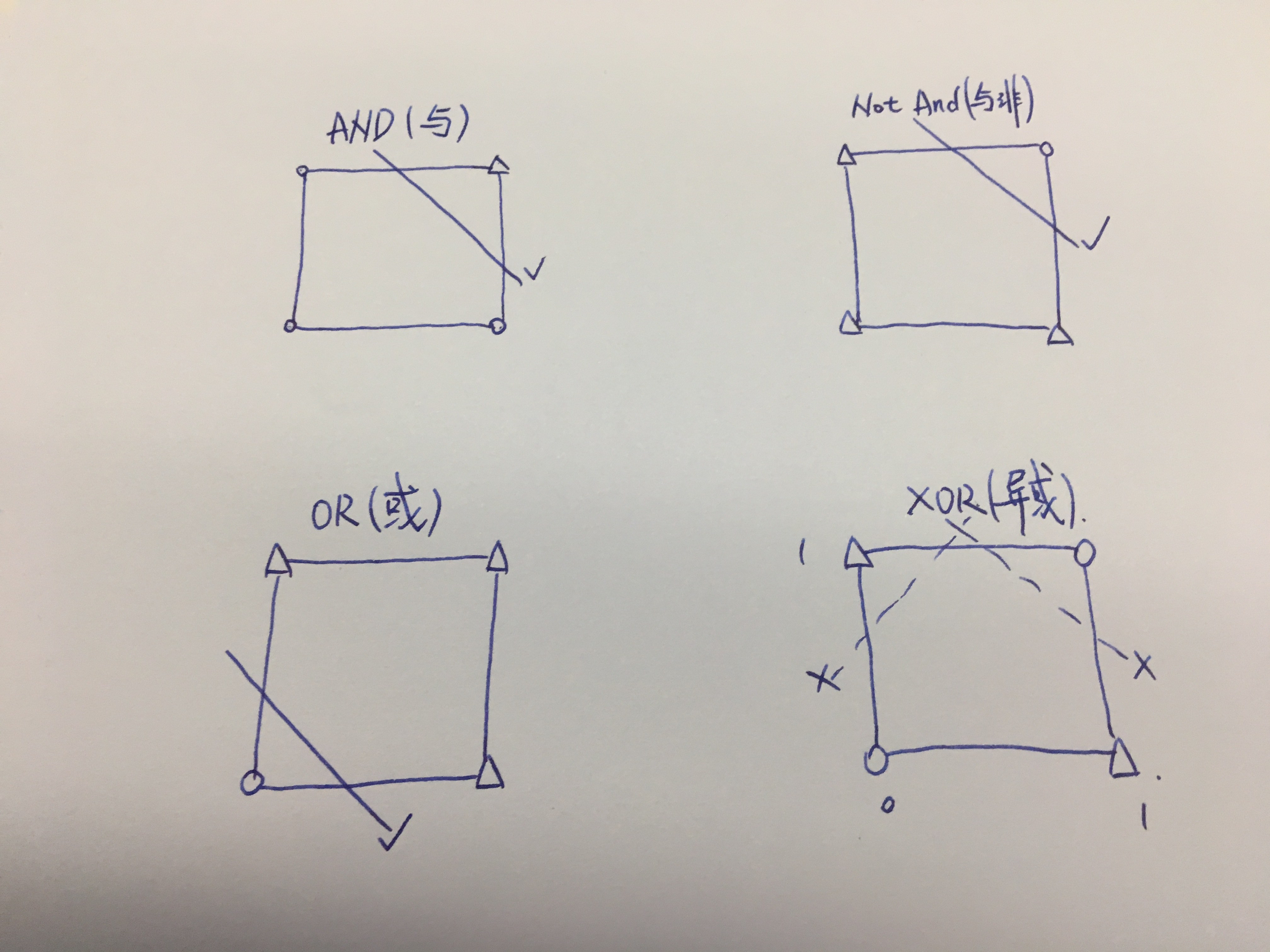
从上图我们可以看出，与（AND），与非（NOT AND），或（OR）等三种情况，都可以找到不止一条直线将各种情况分类开，但是对于异或（XOR），则找不出一条直线，将其进行分类。本质上，异或是一种线性不可分问题。

本文将使用2层神经网络模型，来解决异或问题。具体代码如下：

import tensorflow as tf

# 定义异或问题的输入和标签
X = [[0, 0], [0, 1], [1, 0], [1, 1]]
Y = [[0], [1], [1], [0]]

x_ = tf.placeholder(tf.float32, shape=[4, 2])
y_ = tf.placeholder(tf.float32, shape=[4, 1])

# 定义中间层列维度
HU = 3

# 输入层到中间层的定义
with tf.name_scope("input") as scope:
    W1 = tf.Variable(tf.random_uniform([2, HU], -1.0, 1.0))
    b1 = tf.Variable(tf.zeros([HU]))
    O = tf.nn.sigmoid(tf.matmul(x_, W1) + b1)
    layer1_sum = tf.summary.scalar("liang", O)

# 中间层到输出层的定义 
with tf.name_scope("output") as scope:
    W2 = tf.Variable(tf.random_uniform([HU, 1], -1.0, 1.0))
    b2 = tf.Variable(tf.zeros([1]))
    y = tf.nn.sigmoid(tf.matmul(O, W2) + b2)
    layer2_sum = tf.summary.scalar("jian", y)

# 损失函数使用：最小二乘法，即最小化均方差
with tf.name_scope("train") as scope:
    cost = tf.reduce_sum(tf.square(y_ - y), reduction_indices=[0])
    train_sum = tf.summary.scalar("cost", cost)
    train_step = tf.train.GradientDescentOptimizer(0.1).minimize(cost)

# 实例化Session，并初始化变量
sess = tf.Session()
sess.run(tf.global_variables_initializer())


# 设置运行步长
Ecoches = 5000
for i in range(Ecoches):
    sess.run(train_step, feed_dict={x_ : X, y_ : Y})
    
    if i % 500 == 0:
        result = sess.run(cost, feed_dict={x_ : X, y_ : Y})
        print('Epoch ', i)
        print('Cost ', result)

# 计算预测值与实际值之间的准确率
correcct_prediction = abs(y_ - y) < 0.5
cast = tf.cast(correcct_prediction, "float")
accuracy = tf.reduce_mean(cast)

yy, aa = sess.run([y, accuracy], feed_dict={x_:X, y_:Y})
print("Output: ", yy)
print("Accuracy: ", aa)

运行代码后，看到训练过程日志：

Epoch  0
Cost  [ 1.01291001]
Epoch  500
Cost  [ 0.99675679]
Epoch  1000
Cost  [ 0.97751558]
Epoch  1500
Cost  [ 0.85073531]
Epoch  2000
Cost  [ 0.6944164]
Epoch  2500
Cost  [ 0.1805]
Epoch  3000
Cost  [ 0.05683474]
Epoch  3500
Cost  [ 0.03097299]
Epoch  4000
Cost  [ 0.02076247]
Epoch  4500
Cost  [ 0.01544176]