逻辑回归算法
逻辑回归,即Logistic Regression,简写为LR。
逻辑回归就是这样的一个过程:面对一个回归或者分类问题,选择合适的目标函数(即预测函数,模型),建立代价函数(即损失函数,策略),然后通过优化方法求解出最优的模型参数(算法),然后测试验证我们这个求解模型的好坏。
逻辑回归虽然名字里带了"回归",但是它实际上是一种分类方法,主要用于二分类(即输出只有两种0或1,分别代表两个类别)。
算法标签:回归,二类分类,多类分类。
模型特点:特征条件下类别的条件概率分布,对数线性模型。
模型类型:判别模型。
学习模型:逻辑斯蒂函数。
学习策略:逻辑斯蒂损失(即交叉熵),从极大似然估计或正则化的极大似然估计推导出。
学习算法:梯度下降
1 用途
- 在金融领域,逻辑回归由于可以直接输出原始特征的权重,可以认为是一种可解释的白盒模型,常被用来结合WOE转换,做信用评分卡。
- 在医学领域,逻辑回归用于预测在不同的自变量情况下,发生某病或某种情况的概率有多大。
2 优缺点
| 优点 | 缺点 |
|---|---|
| 速度快,适合二分类问题。 | 对数据和场景的适应能力有局限,不如决策树算法适应性那么强。 |
| 能容易地更新模型,吸收新的数据。 | |
| 简单易于理解,直接看到各个特证的权重。 |
3 基本原理
根据李航在《统计学习方法》里提出的机器学习过程框架:机器学习=模型 + 策略 + 算法,我们可以将逻辑回归表述为下面的过程:
- 寻找一个合适的预测函数(模型),一般表示为
h函数,该函数就是我们需要找的分类函数,它用来拟合特征变量和目标变量。这个过程是非常关键的,需要对数据有一定的分析和探索,知道或者猜测预测函数的"大概"形式,比如是线性函数还是非线性函数。 - 构造一个合适的损失函数(即Cost函数,代价函数,策略),该函数表示预测的输出(
h)与目标变量(y)之间的偏差,可以是二者之间的差(h - y)或者其他的形式。综合考虑所有训练数据的"损失",将Cost求和或者求平均,记为损失函数----J(θ)函数,表示所有训练数据预测值与实际类别的偏差。根据"没有免费的午餐"理论,对于同一个问题而言,所有的模型都是等价的,损失函数实际上表达了人们对于模型的偏好和策略,希望能找到最满意的模型。 - 选择一个合适的算法,计算出可以让损失函数
J(θ)函数最小(根据业务需要,也可能是最大)的参数(θ)集合。机器学习处于数学理论和实际问题的交叉点,很多实际问题翻译成数学方程式之后,通常无法直接严格求解。因此,在处理面向实际问题的数学过程时,往往采用近似拟合的方式。选择合适的算法,类似于在数学理论和实际问题之间寻找一个桥梁,而逻辑回归采用的是梯度下降法(Gradient Descent)。
4 具体过程
4.1 预测函数
预测函数使用Logistic函数,原因在于,若要直接通过回归的方法预测二分类问题,y到底是0类还是1类,最好的函数是单位越阶函数。然而单位越阶函数不连续(GLM的必要条件),而Logistic函数在形式上恰好接近于单位越阶函数,而且单调可微。
Logistic函数(即Sigmoid函数),函数形式为:
$$ g(z) = \frac{1}{1 + e^{-z}} $$
对应的函数图形是一个取值在0和1之间的S型曲线: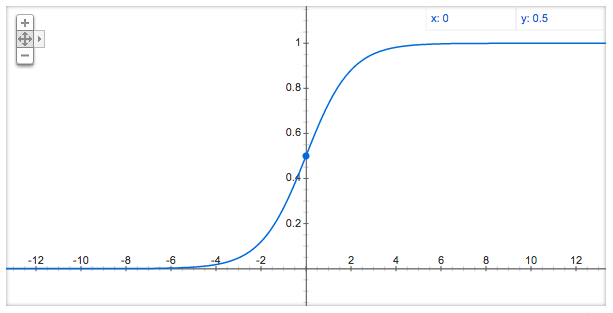
接下来需要确定数据划分的边界类型,对于图2和图3中的两种数据分布,显然图2需要一个线性的边界,而图3需要一个非线性的边界。在逻辑回归算法领域,我们只讨论线性边界的情况。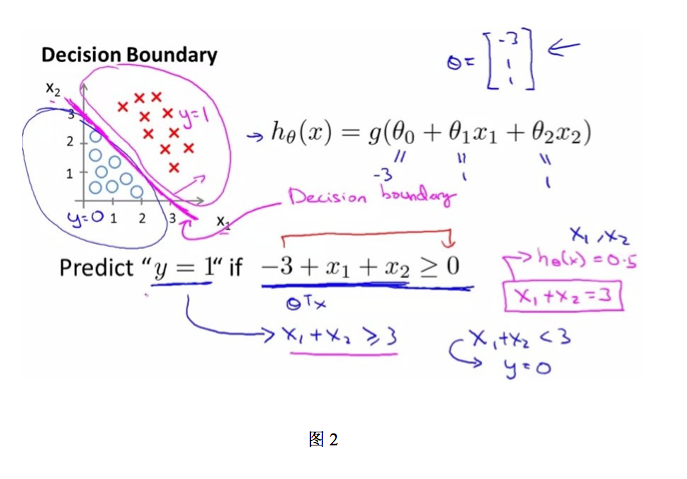
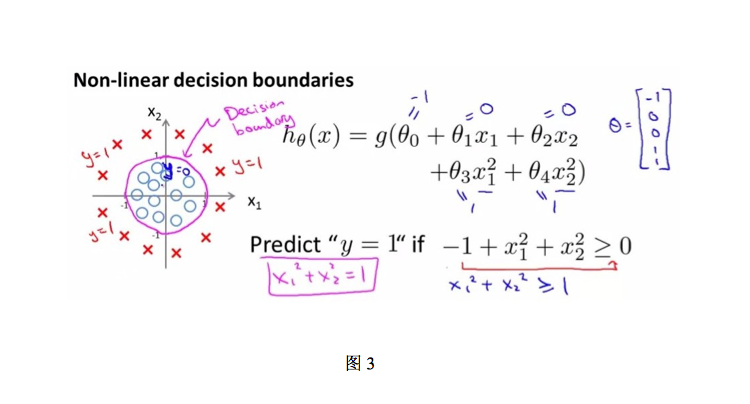
对于线性边界的情况,边界形式如下:
$$ \theta_{0} + \theta_{1}x_{1} + ... + \theta_{n}x_{n} = \sum_{i=0}^{n}\theta_{i}x_{i} = \theta^{T}x $$
构造预测函数为:
$$ h_{\theta}(x) = g(\theta^{T}x) = \frac{1}{1 + e^{-\theta^{T}x}} $$
$h_{\theta}(x)$函数的值有特殊的含义,它标示结果取1的概率(究竟为什么其可以表示概率,在后文我们会进一步探讨),因此对于输入x分类结果为类别1和类别0的概率分别为:
$$ p(y=1|x;\theta) = h_{\theta}(x) $$
$$ p(y=0|x;\theta) = 1 - h_{\theta}(x) $$
综合上面的两种情况,我们得到下面的推导:
$$ p(y|x;\theta) = (h_{\theta}(x))^{y}(1 - h{\theta}(x))^{1-y} $$
4.2 损失函数
在逻辑回归模型中,损失函数通过最大似然估计(MLE)来推导,要正确理解最大似然估计,首先要能从本质上区分概率与统计这两个概念,最大似然估计是个统计工具,其目的是用来估计,某个已经发生的事件,背后需要的模型参数。
比如,我们拿着硬币抛了10次,得到的数据($x_{0}$)是:反正正反正反正正正反。我们想求的正面概率$\theta$是模型参数,抛硬币模型我们可以假设是二项分布,此过程是统计过程。而在概率过程中,正面概率是0.5,不是未知参数,是已知的常识。从这个角度想,概率与统计恰好是相反的两个过程,关于这个问题,我们后文会进一步讨论。
1,我们假设在二类分类中:
结果取类1的概率表示为:
$$ p(y=1|x;\theta) = h_{\theta}(x) = \frac{1}{1 + e^{-\theta^{T}x}} $$
结果取类0的概率表示为:
$$ p(y=0|x;\theta) = 1- h_{\theta}(x) = \frac{1}{1+e^{\theta^{T}x}} $$
在上面两个公式中,x和概率p(可以理解为标签y)都是观测结果,是已知的事实数据,未知数为参数$\theta$,这个问题便转化成统计问题,使用最大似然估计来处理。
2,构建最大似然估计
为了求取使得观察结果(x和y)出现的模型参数$\theta$,我们首先构建似然函数:
$$ \begin{split} L(\theta) &= \prod_{i=1}^{m}P(y_{i}|x_{i};\theta) \\ &= \prod_{i=1}^{m}(h_{\theta}(x))^{y_{i}}(1-h_{\theta}(x))^{1-y_{i}} \end{split} $$
对数似然函数:
$$ \begin{split} l(\theta) &= logL(\theta) \\ &= \sum_{i=1}^{m}(y_{i}logh_{\theta}(x_{i}) + (1 - y_{i})log(1 - h_{\theta}(x_{i})) \end{split} $$
在对数似然函数$l(\theta)$中,$y_{i}$和$x_{i}$作为观察值,都是已知的,因此$l(\theta)$是$\theta$的函数。
到此为止,我们可以用$l(\theta)$作为损失函数,即:
$$ \begin{split} J(\theta) &= l(\theta) \\ &= \sum_{i=1}^{m}(y_{i}logh_{\theta}(x_{i}) + (1 - y_{i})log(1 - h_{\theta}(x_{i})) \end{split} $$
最大似然估计就是求$J(\theta)$取最大值时的$\theta$,其实这里可以使用梯度上升法求解,求得的$\theta$就是要求的最佳参数。
在Andrew Ng的课程中将$J(\theta)$取为下式:,即
$$ \begin{split} J(\theta) &= - \frac{1}{m}l(\theta) \\ &= - \frac{1}{m}\sum_{i=1}^{m}(y_{i}logh_{\theta}(x_{i}) + (1 - y_{i})log(1 - h_{\theta}(x_{i})) \end{split} $$
此时,要使用梯度下降法求解,其中m表示样本个数,$x_{i}$表示第i个样本的内容,$y_{i}$表示i个样本的标签(取值为0和1)。
4.3 学习算法
在逻辑回归模型中,我们使用梯度下降法求解损失函数$J(\theta)$的最小值。
$\theta$更新过程:
$$ \theta_{j} := \theta_{j} - \alpha\frac{\delta}{\delta_{\theta}}J(\theta) $$
其中,$\frac{\delta}{\delta_{\theta}}J(\theta)$的推导如下:
$$ \begin{split} \frac{\delta}{\delta_{\theta}}J(\theta) &= -\frac{1}{m}\sum_{i=1}^{m}(y_{i}\frac{1}{h_{\theta}(x_{i})}\frac{\delta}{\delta_{\theta}}h_{\theta}(x_{i})-(1-y_{i})\frac{1}{1-h_{\theta}(x_{i})}\frac{\delta}{\delta_{\theta}}h_{\theta}(x_{i})) \\ &= -\frac{1}{m}\sum_{i=1}^{m}(y_{i}\frac{1}{h_{\theta}(x_{i})}-(1-y_{i})\frac{1}{1-h_{\theta}(x_{i})})\frac{\delta}{\delta_{\theta}}h_{\theta}(x_{i}) \\ &= -\frac{1}{m}\sum_{i=1}^{m}(y_{i}\frac{1}{h_{\theta}(x_{i})}-(1-y_{i})\frac{1}{1-h_{\theta}(x_{i}))})h_{\theta}(x_{i})(1-h_{\theta}(x_{i}))\frac{\delta}{\delta_{\theta}}\theta^{T}x_{i} \\ &= -\frac{1}{m}\sum_{i=1}^{m}(y_{i}(1-h_{\theta}(x_{i}) - (1-y_{i})h_{\theta}(x_{i}))x_{i} \\ &= -\frac{1}{m}\sum_{i=1}^{m}(y_{i} - h_{\theta}(x_{i})x_{i} \\ &= \frac{1}{m}\sum_{i=1}^{m}(h_{\theta}(x_{i}) - y_{i})x_{i} \end{split} $$
最终,$\theta$更新过程可以写成:
$$ \theta_{j} := \theta_{j} - \alpha\frac{1}{m}\sum_{i=1}^{m}(h_{\theta}(x_{i}) - y_{i})x_{i}^{j} $$
注意:
1) $\alpha$: 代表学习率,用于控制梯度下降的步长。
2) m: 代表样本数量。
3) j: 代表第j轮梯度下降。
4) $\sum_{i=1}^{m}$: 代表在每一轮梯度下降,都要将训练集中所有样本参与计算。
4.4 向量化
向量化(vectorization)是使用矩阵计算来代替for循环,以简化计算过程,提高效率。
向量化过程:约定训练数据的矩阵形式如下,x的每一行为一条训练样本,而每一列为不同的特征取值:
$$ x = \left[ \begin{matrix} x_{1} \\ ... \\ x_{m} \end{matrix} \right] = \left[ \begin{matrix} x_{11} & \cdots & x_{1n} \\ \cdots & \ddots & \cdots\\ x_{m1} & \cdots & x_{mn} \end{matrix} \right],y = \left[ \begin{matrix} y_{1} \\ \cdots \\ y_{m} \end{matrix} \right],\theta=\left[ \begin{matrix} \theta_{1} \\ \cdots \\ \theta_{m} \end{matrix} \right] $$
$$ A = x·\theta=\left[ \begin{matrix} x_{11} & \cdots & x_{1n} \\ \cdots & \ddots & \cdots\\ x_{m1} & \cdots & x_{mn} \end{matrix} \right]·\left[ \begin{matrix} \theta_{1} \\ \cdots \\ \theta_{m} \end{matrix} \right]=\left[ \begin{matrix} \theta_{1}x_{11} + \theta_{1}x_{11} + ... + \theta_{n}x_{1n} \\ \cdots \\ \theta_{1}x_{m1} + \theta_{1}x_{m1} + ... + \theta_{n}x_{mn} \end{matrix} \right] $$
$$ E = h_{\theta}(x) = \left[ \begin{matrix} g(A_{1} - y_{1}) \\ \cdots \\ g(A_{m} - y_{m}) \end{matrix} \right] = \left[ \begin{matrix} e_{1} \\ \cdots \\ e_{m} \end{matrix} \right] = g(A) - y $$
g(A)的参数A为一列向量,所以实现g函数时要支持列向量作为参数,并返回列向量。
$\theta$更新过程可以改为:
$$ \theta := \theta - \alpha\frac{1}{m}\sum_{i=1}{m}(h_{\theta}(x^{i})-y^{i})x^{i}, (j=1...n) $$
综上所述,向量化更新后的步骤如下:
1, 求A = x·$\theta$
2, 求E = g(A) - y
3, 求$\theta := \theta - \alpha x^{T}E$
4.5 正则化
4.5.1 过拟合问题
过拟合即是过分拟合了训练数据,使得模型的复杂度提高,泛化能力较差(对未知数据的预测能力),下面左图即为欠拟合,中图为合适的拟合,右图为过拟合。
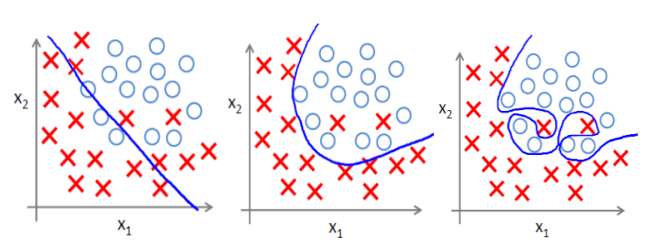
4.5.2 过拟合原因
过拟合问题往往源于过多特征。
解决方法:
1) 减少特征数量(减少特征会失去一些信息,即使特征选取的很好)。
- 可用人工选择要保留的特征。
- 模型选择算法。
2) 正则化(特征比较多时比较有效) - 保留所有特征,但减小$\theta$的大小
4.5.3 正则化方法
正则化是结构风险最小化策略的实现,是在经验风险上加一个正则化项或惩罚项。正则化项一般是模型复杂度的单调递增函数,模型越复杂,正则化项就越大。
正则化项可以取不同形式,在回归问题中取平方损失,就是参数的L2范数,也可以取L1范数。取平方损失时,模型的损失函数变为:
$$ J(\theta) = \frac{1}{2m}\sum_{i=1}^m(h_{\theta}(x_{i}-y_{i})^{2}) + \lambda\sum_{j=1}^{n}\theta_{j}^{2} $$
lambda是正则化项系数:
- 如果它的值很大,说明对模型的复杂度惩罚大,对拟合数据的损失惩罚小,这样它就不会过分拟合数据,在训练数据上的偏差较大,在未知数据上的方差较小,但是可能出现欠拟合的现象。
- 如果它的值很小,说明比较注重对训练数据的拟合,在训练数据上的偏差会小,但是可能会导致过拟合。正则化后的梯度下降算法$\theta$的更新变为:
$$ \theta_{j} := \theta_{j} - \frac{\alpha}{m}\sum_{i=1}^{m}(h_{\theta}(x_{i}) - y_{i})x_{i}^{j} - \frac{\lambda}{m}\theta_{j} $$
5 决策本质
5.1 为什么是逻辑回归?
都说线性回归用来做回归预测,逻辑回归用于做二分类,一个是解决回归问题,一个用于解决分类问题。但很多人问起逻辑回归和线性回归的区别,很多人只知道,逻辑回归就是对线性回归做了一个压缩,将y的阈值从y∈(-∞,+∞)压缩到(0,1)。那么问题来了,问为什么仅仅做了一个简单的压缩,就将回归问题变成了分类问题?这里面蕴涵了什么样的本质?
首先要从数据说起,线性回归的样本的输出,都是连续值,y属于(-∞,+∞),而逻辑回归中y∈{0, 1},只能取0和1。
对于拟合函数也有本质上的差别:
线性回归:$f(x) = \theta^{T}x = \theta_{1}x_{1} + \theta_{2}x_{2} + ... + \theta_{n}x_{n}$
逻辑回归:$f(x) = p(y = 1|x;\theta) = g(\theta^{T}x),\text{其中,}g(z) = \frac{1}{1 + e^{-z}}$
可以看出,线性回归的拟合函数,的确是对f(x)的输出变量y的拟合,而逻辑回归的拟合函数是对为1类的样本的概率的拟合。
5.2 为什么要以1类样本的概率进行拟合呢?
首先,要从logistic函数的本质说起。若要直接通过回归的方法去预测二分类问题,y到底是0类还是1类,最好的函数是单位越阶函数。然而单位越阶函数不连续(GLM的必要条件),而Logistic函数恰好接近于单位越阶函数,而且单调可微。
于是希望通过该复合函数去拟合分类问题:
$$ y = \frac{1}{1 + e^{-\theta^{T}x}} $$
于是有:
$$ ln\frac{y}{1-y} = \theta^{T}x $$
发现,如果我们假设$y=P(y=1|x;\theta)$作为我们的拟合函数,等号左边的表达式的数学意义就是1类和0类的对数几率(log odds)。这个表达式的意思就是:用线性模型的预测结果取逼近1类和0类的几率比。于是,$\theta^Tx = 0$就相当于是1类和0类的决策边界:
当$\theta^{T}x > 0$,则有y > 0.5;若$\theta^{T}x -> +∞$,则y -> 1,即y为1类。
当$\theta^{T}x < 0$,则有y < 0.5;若$\theta^{T}x -> -∞$,则y -> 0,即y为0类。
这个时候就能看出区别来了:
在线性回归中$\theta^{T}$为预测值的拟合函数。
在逻辑回归中$\theta^{T} = 0$为决策边界。
参考
https://blog.csdn.net/u010692239/article/details/52345754
https://blog.csdn.net/u010976453/article/details/78488279